Ecuaciones cuadráticas. Método de factorización
Como un primer método para la resolución de una ecuación cuadrática se presenta el método de factorización. Este es el más rápido de los métodos de resolución y esta básado en una simple propiedad de un producto igual a cero.
Propiedad de un producto igual a cero
Dado que, si el producto de dos números \(mn=0\) una de las dos cantidades es cero o ambas son ceros, esto es \(mn=0 \Longleftrightarrow m=0 ~~{\rm ó}~~ n=0.\)
Como una ecuación cuadrática es un trinomio o un binomo (si es incompleta) su factorización ha tener una de estás formas siguiente.
Formas de factorización para una ecuación de segundo grado.
$$\left\{\begin{array}{l}
x^2+bx+c=0\Longrightarrow(x+h)(x+k)=0~~~~~~~{\rm para}~~hk=c~~{\rm y}~~h+k=b\\
ax^2+bx+c=0\Longrightarrow (ax+h)(ax+k)=0 ~~{\rm donde}~ hk=ac~~y~~h+k=b\\
ax^2-c^2=0\Longrightarrow(\sqrt{a}x+c)(\sqrt{a}x-c)=0~~~~{\rm Diferencia~de~un~binomio.}\\
ax^2+bx=0 \Longrightarrow x(ax+b)=0
\end{array}\right.$$
Resolver una ecuación \(ax^2+bx+c=0\) mediante factorización consiste en factorizar la expresión, igualar a cero ambos factores y despejar la variable.
Para más contenidos clic en y luego clic en la pestaña del contenido deseado.
Raices distintas. Resolver mediante factorización las ecuaciones, \begin{array}{r l}\textcolor{#ff0080}{1.}~~x^2=11x-10&\textcolor{#ff0080}{2.}~~x^2-11x+28=0\end{array}
Simplificando antes de resolver. Resolver mediante factorización las ecuaciones, \begin{array}{l} \textcolor{#ff0080}{1.}~~21x+18=-3x^2~~&\textcolor{#ff0080}{2.}~~4x^2+8x+4=0\end{array}
Trinomios \(ax^2+bx+c=0\). Resolver por factorización las ecuaciones, \begin{array}{r l l} \textcolor{#ff0080}{1.}~~10x^2=3-13x&\textcolor{#ff0080}{2.}~~7x^2-19x-6=0 &\textcolor{#ff0080}{3.}~~27+3x-2x^2=0 \end{array}
Diferencias de cuadrados. Resolver por factorización las ecuaciones cuadráticas siguientes: $$\begin{array}{l} \textcolor{#ff0080}{1.}~~49x^2-3=0~&\textcolor{#ff0080}{2.}~~16x^2-25=0~\\ \textcolor{#ff0080}{3.}~~\frac{x^2}9-121=0~& \textcolor{#ff0080}{4.}~~\frac{25x^2}{16}-\frac{5}{81}=0~~~~~~~\end{array}$$
Máximo común divisior. Determinar las raíces de las ecuaciones, \begin{array}{l} \textcolor{#ff0080}{1.}~x^2=13x~~&\textcolor{#ff0080}{2.} -4x^2=-8x\\ \textcolor{#ff0080}{3.}~~5x^2-55x=0~~&\textcolor{#ff0080}{4.}~~175x^2-1183x=0\end{array}
Una expresión racional. Determinar los valores de \(x\) que hacen verdadera la expresión, $$\frac{3}{x-4}+\frac{12}{x-3}=\frac{11}{2}$$
Dimensiones. 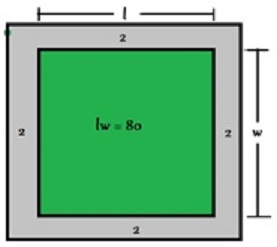 Un jardín rectangular está rodeado por un sendero de grava que mide dos pies más que las dimensiones del jardin. El área que cubre el jardín es de \(80 {\rm ft^2}\), y el área que abarca la acera es de \(100 {\rm ft^2}\). Determinar las dimensiones del jardín. (Dibujo no está a escala).
Un jardín rectangular está rodeado por un sendero de grava que mide dos pies más que las dimensiones del jardin. El área que cubre el jardín es de \(80 {\rm ft^2}\), y el área que abarca la acera es de \(100 {\rm ft^2}\). Determinar las dimensiones del jardín. (Dibujo no está a escala).
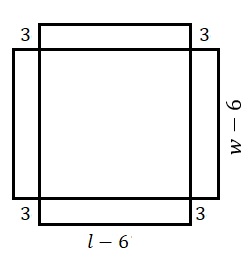
Taller. En el taller de mecanizado se desea construir un recipiente en forma de caja prismática sin tapa (ver figura) la cual debe tener un volumen \(4704{\rm{in}}^3\) con una pequeña hoja cuadrada de aluminio cortando un cuadrado de seis pulgadas de cada esquina y doblando los lados como muestra la figura (no está a escala). Determine la longitud de uno de los lados de la hoja de aluminio original.
Taller. En el taller de mecanizado se desea construir un recipiente en forma de caja prismática sin tapa (ver figura) la cual debe tener un volumen \(504{\rm{cm}}^3\) con una pequeña hoja rectangular de aluminio cortando un cuadrado de tres pulgadas de cada esquina y doblando los lados hacia arriba como muestra la figura (no está a escala). Si el área de la lámina después de cortar los cuadrados es de \( 324{\rm cm}^2\) determine la longitud de uno de los lados de la hoja de aluminio original.
Dimensiones de una jardinera. Como parte del remozamiento de uno de los pabellones de la escuela se tiene un presupuesto de \($96000\) para la construcción de una jardinera rectangular en dicho pabellón. Esta será sembrada de rosas y cercada en todo su alrededor. Para esto se ha contratado una compañía la cual ofrece una cerca cuyo costo es de $200 por metro lineal y para las rosas $200 por metro cuadrado. Determinar la longitud que debe tener la jardinera para que sea posible usar todo el presupuesto, además considere si es posible o no que la jardinera esté dentro de un espacio de \(21m\) por \(19m\) al usar todo el presupuesto.
Costo de una excursión. Cierto número de estudiantes deciden realizar una excursión la cual tiene un costo total de \($18000\), distribuyendo el costo de manera uniforme entre todos los participantes. Si en el último instante, tres personas deciden no ir, el costo para cada persona se aumenta en \($300\). Determinar cuántas personas van a la excursión.
Rapidez. Un motociclista recorre \(60km\) a rapidez constante. Si hubiera ido \(10\frac{km}{h}\) más rápido, habría reducido el tiempo de viaje en \(1h.\) Determine la rapidez del motociclista.
Plantar un jardín. Se desea plantar un jardín rectangular con un perímetro de \(76m\) y un área de \(360m^2\). Determine las dimensiones del jardín.
Dimensiones de un terreno. Un terreno rectangular de \(20m\times16m\) está rodeado por una acera de ancho uniforme. Si el área que abarca la acera es de \(460m^2\) determinar el ancho de la acera.

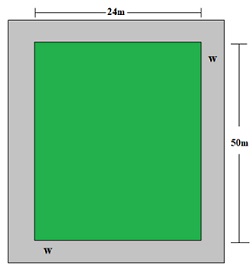 Dimensiones. Un área rectangular cubierta de césped de \(50m\) por \(24m\) está rodeada por una acera de ancho uniforme como muestra la figura (no está a escala). Si el área que abarca la acera es \(480m^2\), determinar el ancho de la acera.
Dimensiones. Un área rectangular cubierta de césped de \(50m\) por \(24m\) está rodeada por una acera de ancho uniforme como muestra la figura (no está a escala). Si el área que abarca la acera es \(480m^2\), determinar el ancho de la acera.